
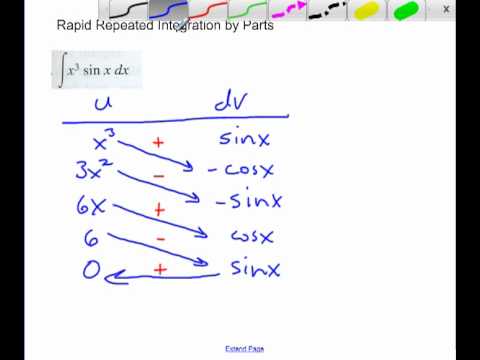
Some integrals require repeated use of the integration by parts formula. Use integration by parts on $g$ such that the integral over $h$ disappears.Įxample: Let $f(x) = (1 + 2x^2) e^$ in terms of $I_n$), which results in a structure which is easier to remember and a more pleasant way of organizing the computations. Use a tabular method to perform integration by parts. A TABULAR METHOD FOR REPEATED INTEGRATION BY PARTS Integrals of the form p(x)f(x)dx where p(x).

The product of two functions, $f = g \cdot h$. Integration by parts tabular method is a short method for integration to solve the integral problem quickly, instead of using the lengthy and tedious. Can anyone help me with this limit, I’m getting 8 but the answer is supposed to be -2. However, let us integrate this new integral by parts. Assume you are to integrate some function that can be written as The integration by parts tabular method is also called the DI method to solve integration problems quickly by forming three columns, the first one for Alternative sign, the second column for Derivative function and the third column for Integration function. Section 8.


 0 kommentar(er)
0 kommentar(er)
